Multi-layer Neural Network Implementaion - 1 보고오기
3.9 L2 & L1 Regularization
Regularization은 일종의 penalty 조건으로 cost function이 작아지는 쪽으로 진행할 경우 단순하게 작아지기만 하면 특정 가중치 값들이 커지면서 오히려 결과에 악영향을 끼치는 경우가 발생한다.
위 식을 통해 학습의 방향이 단순하게 원래 cost function의 값인 C0가 작아지는 방향으로만 진행되는 것이 아니라 w값들 역시 최소가 되는 방향으로 진행하게 된다. 이때 cost function을 w에 대해서 편미분을 하게되면 새로운 가중치는 아래와 같이 결정된다.
이때 L2 Regularization은 weight decay에 의해 특정 가중치가 비정상적으로 커지고 이로인해 학습에 악영향을 끼치는 것을 방지할 수 있다.
L1 Regularization은 w값이 2차항 대신 1차항이 오게된다. 마찬가지로 cost function을 w에 대해서 편미분을 하게되면 새로운 가중치는 위와 같이 결정된다. 이를 통해 weight값을 줄이는 것이 아니라 w의 부호에 따라 상수 값을 빼주는 방식으로 Regularization을 하게 되며 작은 가중치들은 0으로 수렴하고 중요한 가중치들만 남게 된다. 따라서 몇 개의 의미있는 값을 얻어내고자 할 경우 L1이 효과적이다.
다음은 실제 구현한 테스트 결과이다. SGD + Cross-Entropy + Softmax에 Lambda 값을 5.0으로 지정하고 나머지 조건은 기존과 동일하다.
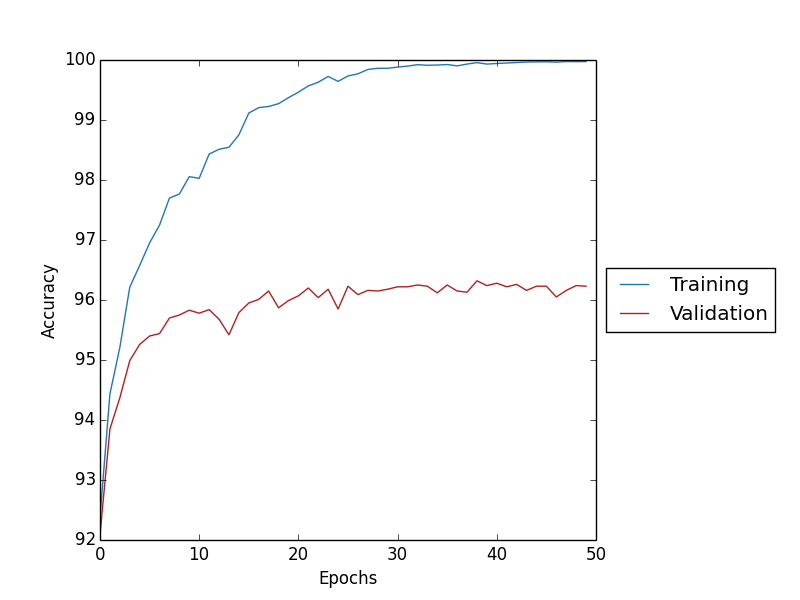
Cross-entropy와 Softmax를 사용해서 Accuracy를 구한 그래프이다.
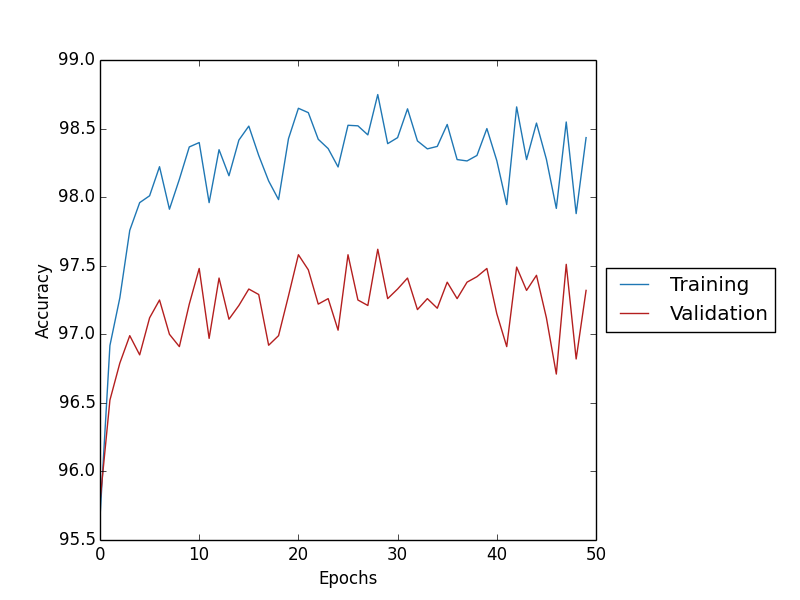
Cross-entropy와 Softmax, L2를 사용해서 Accuracy를 구한 그래프이다.
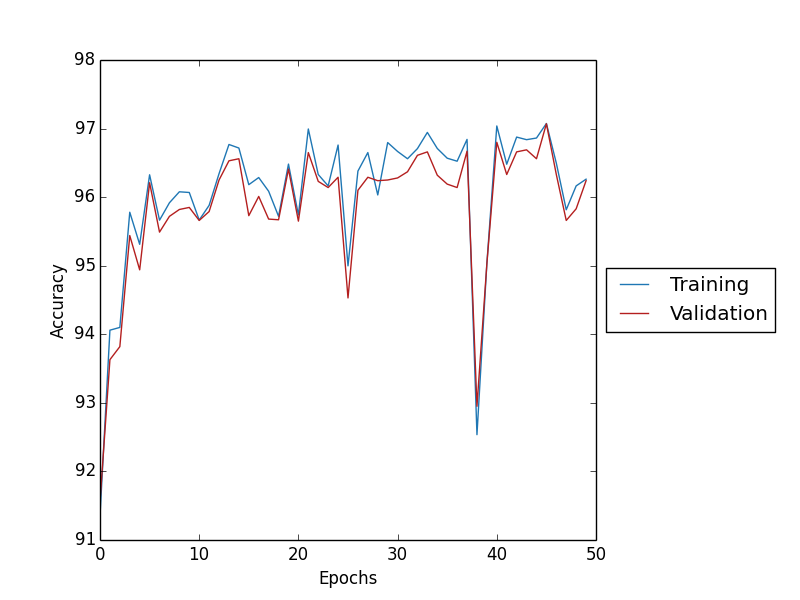
Cross-entropy와 Softmax, L1을 사용해서 Accuracy를 구한 그래프이다.
그래프를 통해 비교해보면 L2, L1을 적용한 결과에선 Overfitting이 감소한것을 확인할 수 있다. 또한 L2의 경우 Overfitting이 감소하면서 Test Data Accuracy가 97.21%로 Cross-entropy와 Softmax를 사용 96.33%에 비해 증가 한 것을 확인할 수 있다.
3.10 Dropout
Dropout은 L2, L1과 같이 Overfitting 문제를 피하기 위한 방법이며 학습을 할때 모든 뉴런이 학습을 수행하는 것이 아닌 일부 뉴런들을 생략(dropout)하고 줄어든 신경망을 통해 학습을 한다.
mini-batch 구간 동안 dropout된 망에 대한 학습을 끝내면 다시 무작위로 다른 뉴런들을 dropout하면서 반복적으로 학습을 수행한다.
이러한 과정을 통해 Voting 효과처럼 mini-batch마다 이루어 지는 무작위 뉴런의 학습에 의해 평균 효과를 얻을 수 있으며 특정 뉴런의 바이어스나 가중치가 큰 값을 가지지 못하도록 해서 학습에 악영향을 미치는 것을 방지 할 수 있다.
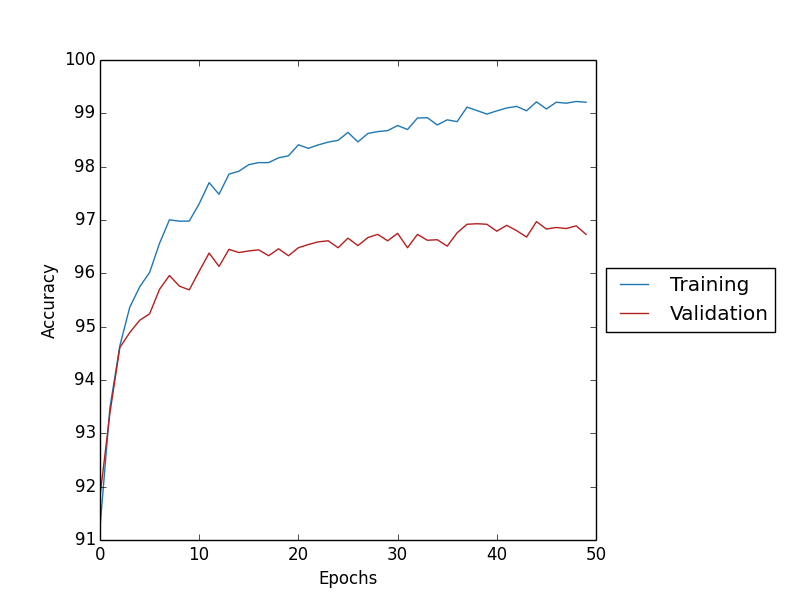
Dropout의 비율은 0.8이며 결과 그래프를 확인하면 Overfitting이 감소한 것을 확인할 수 있다.
3.11 Weight initialization
Xavier 초기화 방법을 이용하여 Weight initialization을 했다. Xavier 초기화 방법은 input 뉴런의 수에 맞게 조정한다. 뉴런마다 이전 레이어에서 들어오는 input 뉴런의 수가 많다면 파라미터의 초기화 값을 낮추어서 너무 큰 값이 되지 않도록 하고 반대로 뉴런의 수가 적다면 초기화 값을 높히는 역할을 한다.
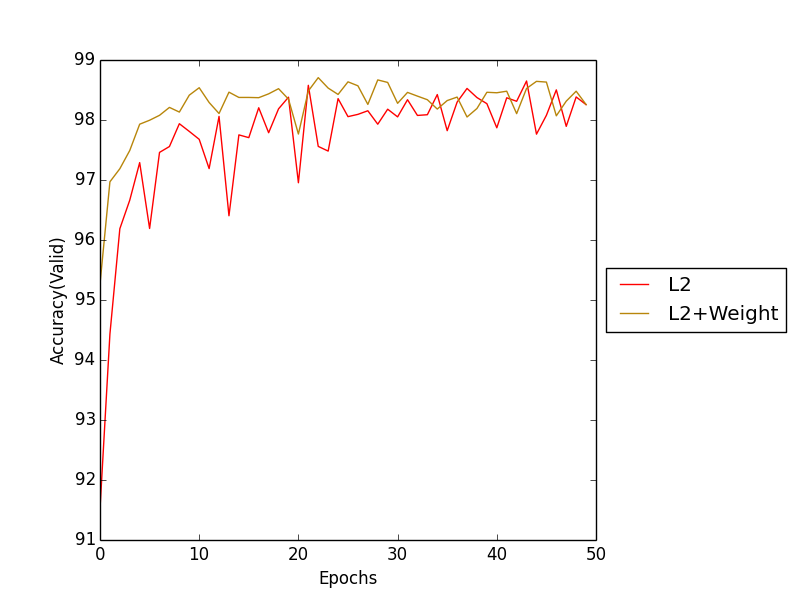
결과 그래프를 확인하면 L2에 비해 Weight initialization을 해준 학습의 속도가 더 빠른것을 확인할 수 있다.
4. Result
실험한 학습 데이터를 기반으로 Test Data를 input으로 넣어 측정한 Accuracy를 표로 나타내었다. 이를 통해 Cross-Entropy와 Softmax를 사용하는 방법이 정확도 향상에 효과가 있으며 특히 L2 Regularization + Weight Init은 97.23%로 가장 높은 정확도를 나타냈다.
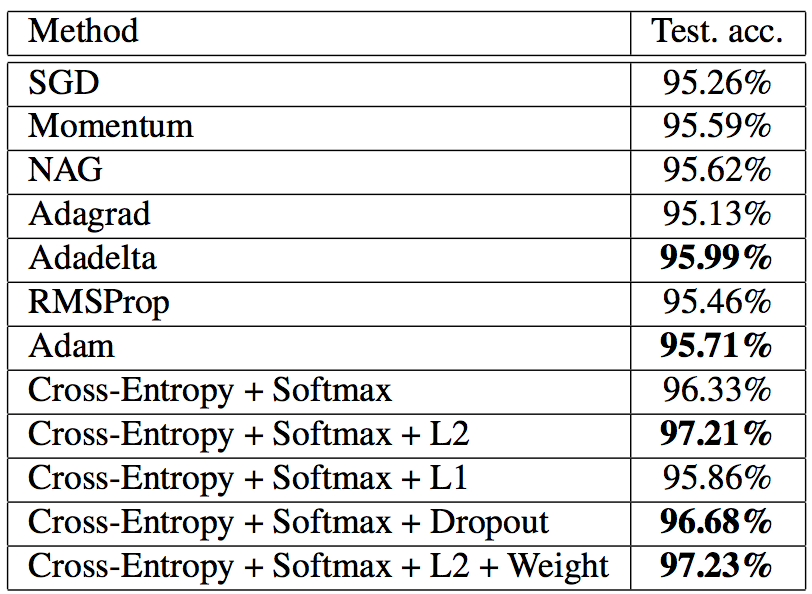
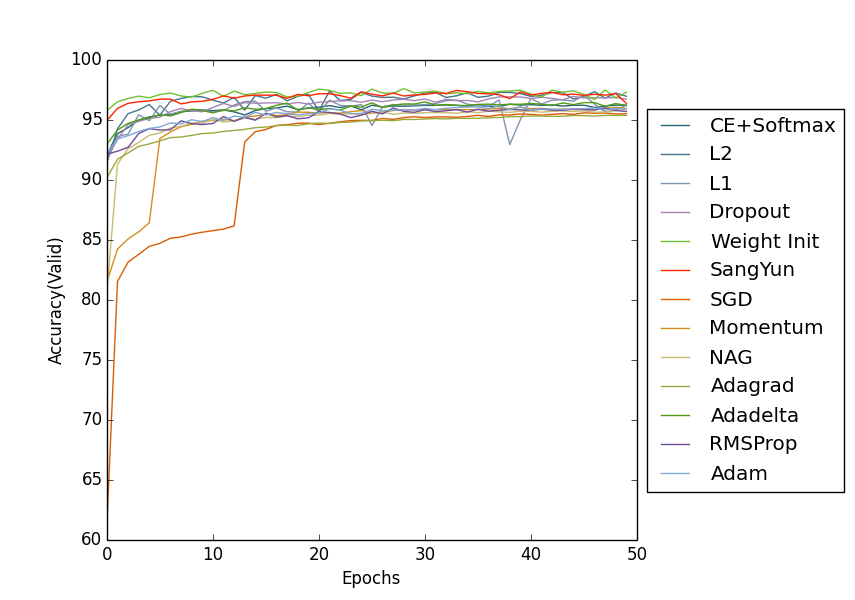
784개의 input layer, 60개의 hidden layer, 10개의 output으로 신경망을 구축했으며 학습방법은 Stochastic Gradient Descent(SGD)로 Learning Rate = 0.5, Epochs = 50, Mini batch size = 10, L2의 Lambda = 5.0, Dropout Rate = 0.8, 5000개의 Training data, 10000개의 Validation data, 10000개의 Test data로 이루어진 MNIST dataset을 사용했다.
신경망에 적용된 학습방법은 Sigmoid Activation Functions으로 SGD와 Weigh initialization, Cross-Entropy, Softmax, Dropout, L2 Regularization을 사용했다.
SangYun은 SGD + Cross-Entropy + Softmax + L2 + Dropout + Weight를 이용해 학습한 결과이다. 그래프를 살펴보면 Validation data의 Accuracy는 Weight Init과 SangYun이 가장 빠른 학습 속도를 보이고 있다.
특히 SGD + Cross-Entropy + Softmax + L2 + Weight은 가장 높은 Test data 정확도 97.23%를 나타내며 학습 속도 또한 가장 빠른것으로 나타났다.
실험 결과 Multi-layer Neural Network에 대한 이론뿐만 아니라 실제 구현을 해보며 이론에 대한 결과물을 확인할 수 있었으며 인공신경망에 대해 이해할 수 있는 좋은 경험이었다.
