1. Introduction
목적은 인공신경망을 직접 구현하고 각각의 학습법에 따라 얼마만큼의 정확도의 차이를 보이는지를 알아본 후 이를 통해 가장 좋은 퍼포먼스를 가진 네트워크를 도출해 내는 것이다.
Multi-layer Neural Network로 구현하며 input layer, hidden layer, output layer로 이루어져 있다.
학습 데이터는 MNIST digits recognition를 사용하며 60000개의 필기로 작성한 숫자 이미지와 정답 셋이 주어진다.
학습데이터는 Multi-layer Neural Network source code에 mnist.pkl.gz 파일이다.
이 중 50000개는 트레이닝 데이터이며 나머지 10000개는 검증 데이터이다.
테스트 데이터는 학습 데이터에 없는 이미지로 10000개를 제공한다.
각 이미지는 28*28의 크기이다. 이 데이터는 0 부터 255의 RGB값으로 정의되어 있다.
이를 0 과 1사이의 값으로 정규화해서 사용한다.
input layer에 입력하기 위해 784개의 input neuron을 생성한다.
hidden layer는 60개의 neuron을 지정했다.
output layer는 0 부터 9까지의 숫자를 표현할 수 있도록 10개의 neuron을 지정했다.
학습 방법에 따른 정확도의 차이를 확인하기 위해 총 50번의 epoch을 설정하고 이에 따른 cost와 accuracy을 측정하여 그래프화 했다.
테스트 결과에 대한 분석은 3장의 내용을 살펴보면 확인 할 수 있다. 4장에서는 테스트를 통해 도출한 결과값으로 가장 좋은 퍼포먼스를 나타내는 네트워크를 설계하고 테스트했다.
MNIST 학습데이터를 이용해 인공신경망에 학습시킨 결과를 바탕으로 작성되었다.
각각의 학습 방법에 따라 얼마만큼의 정확도를 보이는지에 대해 그래프, 도표 등을 이용해 비교한다.
2. Dataset
Multi-layer Neural Network 구현을 위한 프로그래밍 언어는 Python 2.7을 사용했으며 행렬계산 등 시간복잡도가 많이 요구되는 연산을 빠르게 수행하기 위해 Python의 수학 연산 라이브러리인 numpy를 사용했다.
MNIST 데이터셋 파일을 읽기 위해 Python의 파일 입출력 라이브러리인 cPickle을 사용했다.
MNIST database는 필기 숫자들의 그레이스케일 28*28 픽셀 이미지를 보고 0부터 9까지의 모든 숫자들에 대해 이미지가 어떤 숫자를 나타내는지 판별하는데 필요한 database이다.
train-images-idx3-ubyte.gz와 train-labels-idx1-ubyte.gz로 총 60000개 중 50000개의 트레이닝 이미지와 정답셋을 제공하며 나머지 10000개는 검증 데이터로 사용한다.
t10k-images-idx3-ubyte.gz, t10k-labels-idx1-ubyte.gz로 10000개의 테스트 이미지와 정답셋을 제공한다.
이미지 파일의 데이터는 magic number, number of images, number of rows, number of columns로 해당 파일의 정보를 제공하고 나머지 공간은 전부 pixel 데이터로 채워져있다.
pixel은 0부터 255의 RGB데이터로 저장되어 있다. 정답셋은 magic number, number of items로 입력될 정답셋의 갯수를 제공하고 나머지는 label로 정답으로 채워져 있다.
label은 0부터 9의 숫자 결과값으로 저장되어 있다. MNIST database를 더 빨리 불러오기 위해 RGB값이 0부터 1사이의 값으로 정규화된 mnist.pkl.gz라는 파일로 학습과 테스트를 실시했다.
3. Implementation
784개의 input layer, 60개의 hidden layer, 10개의 output layer로 구성되어 있으며 Activation Function은 Sigmoid를 사용한다. 학습시간의 단축을 위해 Stochastic Gradient Descent(SGD)를 사용했으며 mini-batch size는 10이다. 학습한 Gradient descent optimization algorithm은 Momentum, Nesterov accelerated gradient, Adagrad, Adadelta, RMSprop, Adam이 있다. Learning rate = 0.5 이며 50 Epoch 동안 학습을 실시했다.
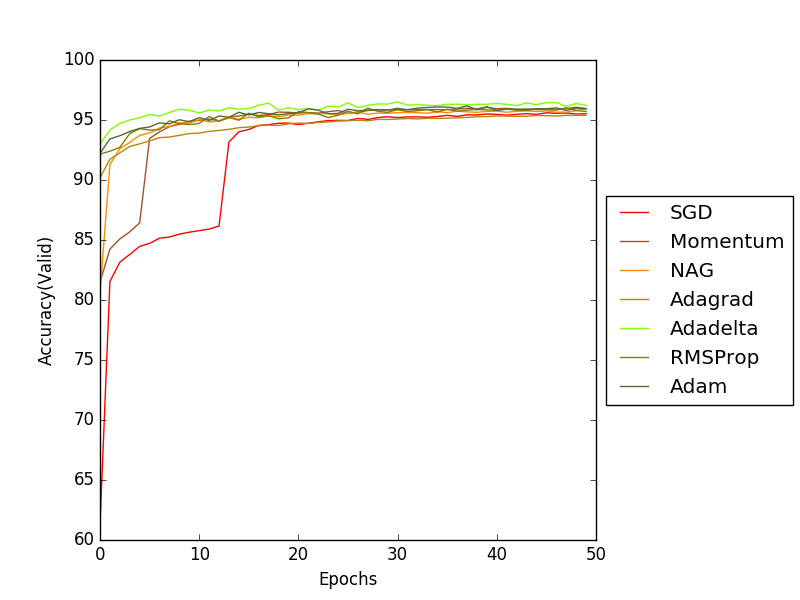
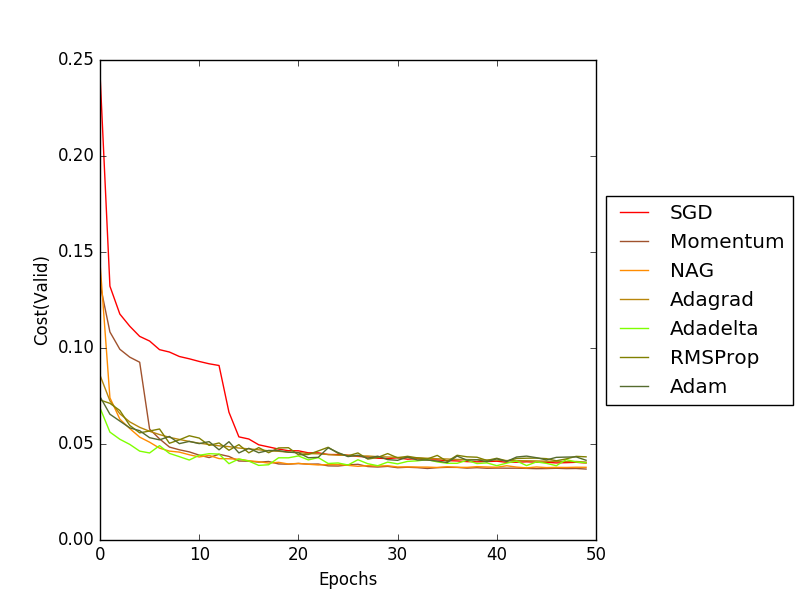
그래프를 통해 SGD, Momentum, Nesterov accelerated gradient(NAG), Adagrad, Adadelta, RMSProp, Adam 순으로 비교 분석을 해보았다.
3.1 Stochastic Gradient Descent(SGD)
SGD는 가장 오랜시간을 거쳐서 Accuracy가 증가하는 것을 볼 수 있다. 다음은 SGD에서 사용한 weight update 수식이다. w는 weight를 나타내며 dx는 Gradient를 나타낸다.
Cost 그래프를 통해 살펴보면 Local Minima의 전형적인 형태가 나타났고 이를 넘어가기 위해 오랜 시간을 소모하게된 것을 볼 수 있다.
3.2 Momentum
Momentum은 이러한 Local Minima를 극복하기 위해 진행 방향으로 가속도를 추가하여 연산하는 과정을 거친다.
여기서 상수 momentum의 값은 0.5로 설정하여 학습 했다. 그래프를에서 가속도의 추가를 통해 SGD보다 더 빠르게 Cost가 감소하는 것을 확인할 수 있다.
3.3 Nesterov accelerated gradient(NAG)
Nesterov accelerated gradient과 Momentum을 비교해서 설명하면 그림의 왼편에 보이는 Momentum update의 경우 빨간 원에서 Gradient를 계산하여 움직이고 해당 위치에서 momentum만큼 이동하게 된다.
Nesterov momentum update의 경우 빨간 원에서 momentum만큼 이동하고 이동한 위치에서 Gradient를 적용한다. 학습에 사용한 momentum은 0.5이며 그래프를 확인해보면 Momentum보다 더 빠르게 Cost가 감소하는 것을 확인할 수 있다.
3.4 Adagrad
Adagrad는 Adaptive gradient algorithm으로 시간에 따른 Gradient를 제곱값을 이용해 학습률을 조정하는 알고리즘으로 잘 업데이트 되지 않는 파라미터의 학습률을 높이기 때문에 쉽게 0이 될 수 있는 데이터에서 유용하다.
cache가 계속 0이 나왔을 경우 분모가 0이 되는 것을 막기 위해 별도의 상수를 설정해준다. 보통 초반에 학습이 빨리 이루어 지지만 학습이 계속되면 cache가 누적되어 w값이 작아지게된다.
3.5 Adadelta
Adadelta은 Adagrad의 문제점인 학습률이 빨리 떨어지는 단점을 보완하기 위해 모든 Gradient의 제곱값을 이용하지 않고 가장 최근의 Gradient값들과 Decay rate(dr)를 설정하여 급하게 감소하는 학습속도를 보완했다.
사용한 Decay rate = 0.5이며 그래프 결과상에서 Adagrad보다 Adadelta가 더 빠르게 학습되는것을 확인할 수 있다.
3.6 RMSProp
RMSProp은 Adadelta에서 Hinton 교수의 주장에 의해 Decay rate = 0.9, 0.99, 0.999 중 하나로 지정해 사용한다. 여기선 0.9를 사용했다.
그래프 결과상에서는 Adagrad보다 빠르고 Decay rate = 0.5인 Adadelta보단 느리게 학습되는것을 확인할 수 있다.
3.7 Adam
Adam은 RMSProp과 Momentum을 합친 알고리즘으로 beta1은 Momentum을 의미하고 beta2는 Decay rate를 의미한다.
일반적으로 beta1 = 0.9 beta2 = 0.999를 사용하지만 여기선 beta1 = 0.5, beta2=0.555를 사용했다.
그래프 결과상에서 Adadelta보다 느리고 RMSProp보다 빠른 학습속도를 확인할 수 있다.
3.8 Cross-Entropy cost function & Softmax
지금까진 Quadratic Cost를 사용해 에러를 측정했다. 하지만 Quadratic Cost와 sigmoid를 같이 사용하는 경우 error signal이 너무 작아질 경우 학습이 잘 되지 않는 현상이 발생하게 된다.
예를 들자면 하나의 뉴런이 있다 가정하고 가중치는 w, 바이어스는 b, 활성함수는 sigmoid를 사용한다고 하자.
이때 입력 x를 가하면 z = wx + b가 되고 sigmoid를 거쳐 출력 a가 나오게 된다.
이때 나와야 할 값이 y라고 할 경우 Quadratic cost function은 다음과 같은 식을 나타내게 된다.
여기서 (y-a)는 오차가 되고 Backpropagation을 통해 C를 가중치와 바이어스에 대해서 편미분을 하게 된다.
와 같은 결과가 나오게 된다. 이때 sigmoid 함수의 미분값을 곱하는 부분에서 문제가 발생한다.
z가 0일때 최대값을 갖고 0으로부터 멀어질 수록 0에 수렴하는 작은 값으로 가게 되는데 결국 아주 작은 값을 곱해주는 형태로 변하게 되어 학습 속도 저하가 일어나게 된다.
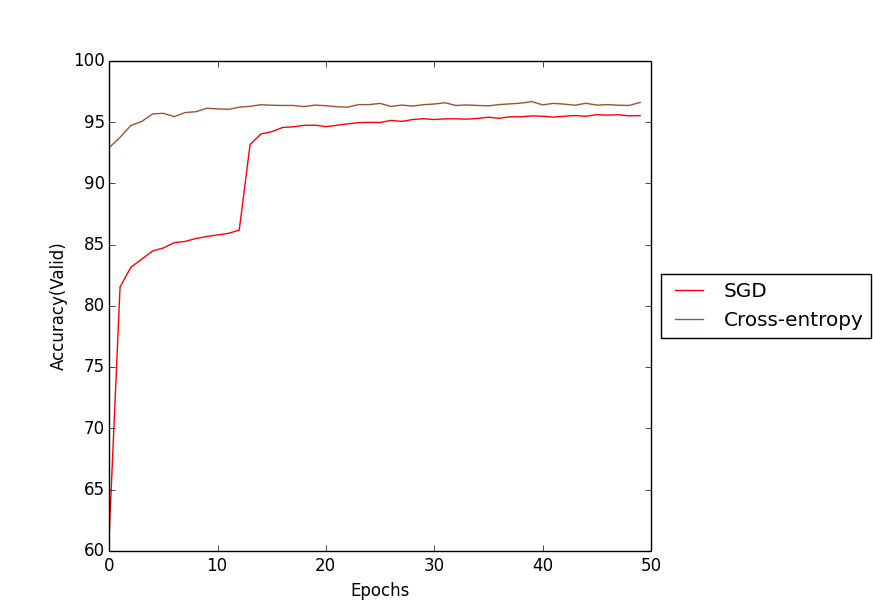
SGD를 통해 학습했으며 Cost function만 Quadratic과 Cross-entropy로 나누어서 테스트한 Accuracy 그래프 이다.
이 그래프로 Cross-entropy cost function의 학습속도가 더 우수함을 확인 할 수 있다.
Cross-Entropy cost function은 이를 해결하기 위해 다음과 같은 cost function을 사용한다.
이렇게 도출한 식을 통해 계산해보면 기대값과 실제 출력의 차에 비례하는 결과를 얻을 수 있게 되며 Quadratic cost function보다 더 빠른 속도로 학습을 할 수 있게된다.
Softmax는 위와 같은 수식에 의해 출력값이 계산된다. Softmax는 출력값이 다른 뉴런의 출력값과의 상대적인 비교를 통해 확률의 형태로 나타나며 이를 통해 확률이 가장 높은 값이 분류된 결과 값이라는 걸 알 수 있다. 따라서 신경망에서 output layer에 많이 사용된다.
다음은 Cross-Entropy cost Function과 hidden layer에 sigmoid를 output layer에 Softmax를 사용한 결과와 Quadratic cost를 사용한 SGD, Cross-Entropy만 사용한 Training data accuracy와 Cost를 비교한 그래프이다.
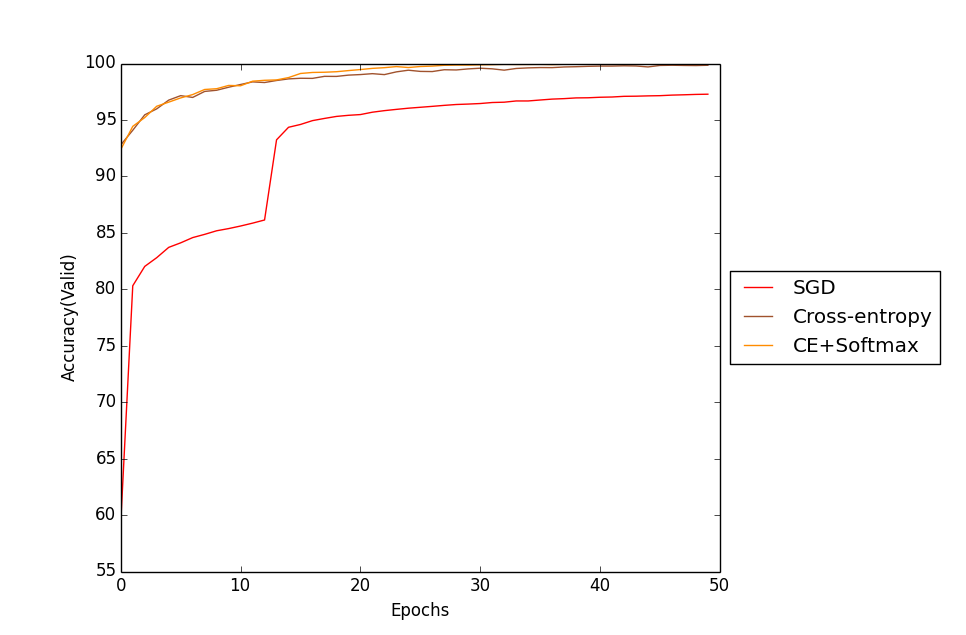
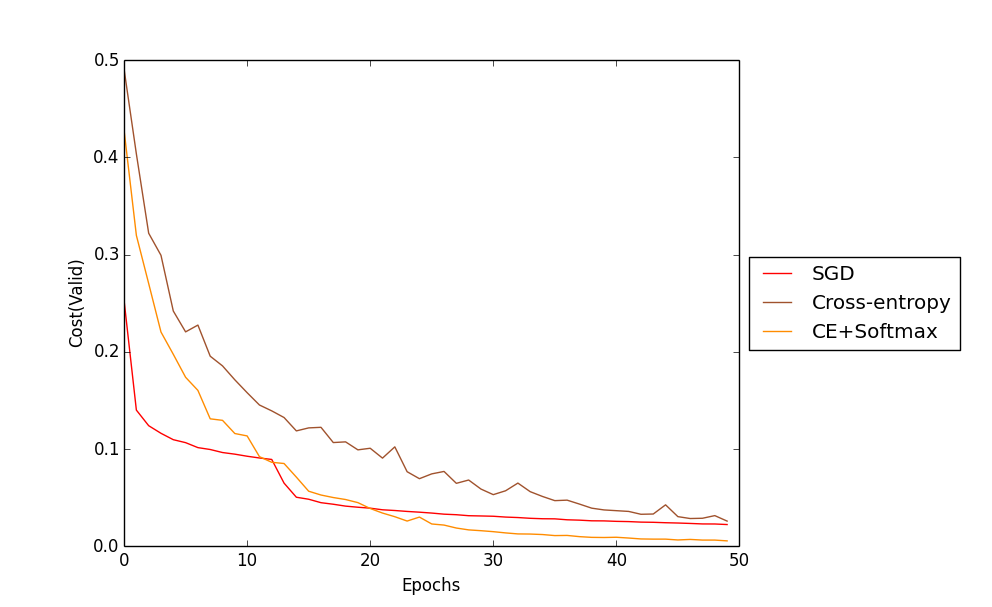
그래프를 통해 Cross-Entropy와 Softmax를 함께 사용할 경우 가장 좋은 학습성능을 나타내는 것을 확인할 수 있다.
나머지 알고리즘과 결과 설명은 Multi-layer Neural Network Implementaion - 2에서 마저 작성한다.
